如何在Cesium中計算動目標姿態
背景:在三維場景中,我們經常會需要模擬一些運動的目標,比如行駛中的汽車,飛行中的飛機,在軌運行的衛星等等。我們可以動態的設置模型或者圖元的位置來使其運動起來,單純的位置移動比較容易實現,但運動姿態(例如汽車的朝向)則需要我們進行計算,相對于位置來說姿態的計算會復雜一些。
本文通過坐標系介紹、目標位置計算、目標姿態計算三部分循序漸進地講解了如何實現三維場景中動目標姿態的計算。
1.球心坐標系、模型坐標系
球心坐標系是指坐標原點與地心重合,Z軸垂直赤道面,X軸朝向(東經0°,北緯0°),Y軸朝向(東經90°,北緯0°),如圖1所示。
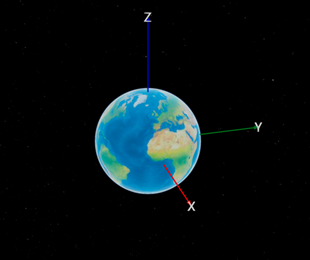
圖1 Cesium球心坐標系
模型坐標系是建模軟件在建模過程中或者在程序構建圖元時使用的坐標系,為了方便建模,一般球狀物體的原點都在物體中心,游戲角色模型原點一般位于腳部。
在三維場景中直接加載模型,模型中心點會與地心重合,也就是說模型坐標(0,0,0)會和球心坐標(0,0,0)點重合。如果我們想要把模型放置到地球表面某一點,就需要經過一個矩陣轉換把模型的頂點坐標轉換到地球表面。
當然你也可以在建模的時候就把模型建立在目標位置的世界坐標上比如(100,0,0),但是當你想讓模型繞中心點旋轉的時候,模型會沿著世界坐標的原點作半徑為100的圓周運動,如果要達到正確的效果,你就需要先把模型移到世界原點,旋轉,然后再移回來,操作起來會比較麻煩。
2. 目標位置計算
接下來再了解一下,Cesium中是如何把模型放置到地球表面的指定位置處。我們一般都是使用的地理坐標經度、緯度、高度,比如(108.0,30.0,1000.0),通過Cesium.Cartesian3.fromDegrees(108,30,1000)轉換得到其對應的世界坐標,然后通過一個四維矩陣對模型進行平移和旋轉,Cesium中提供了多種世界坐標轉換為矩陣的接口,不同的轉換接口,放置到地球表面模型的姿態角度不同。如圖2所示,轉換到地球高空某位置的飛機會有各種姿態,其中我們經常用到的“東北天”坐標是中間ClassicalEastNorthUp local Frame所示效果,模型坐標系的X軸朝向正東方向,Y軸朝向正北方向,Z軸朝向垂直于地球表面向上方向。
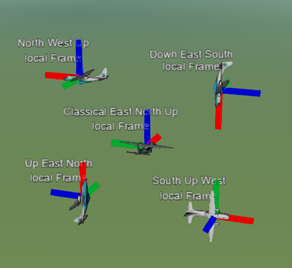
圖2 飛機的各種姿態
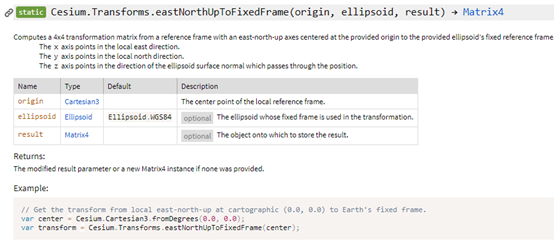
圖3 “東北天”轉換接口
圖3中的eastNorthUpToFixedFrame函數是用于處理“東北天”姿態使用的的接口,其中的參數的含義如下:
a) Origin是模型位置的世界坐標,可以通過Cesium.Cartesian3.fromDegrees(108,30,1000)轉換得到。
b) ellipsoid為參考的橢球體;
c) result為返回的矩陣,該矩陣中包含了模型的旋轉角度與平移距離。
3.目標姿態計算
了解了以上的知識點后,我們就可以正式開始介紹如何計算動目標姿態了。圖4是我們模擬的兩個時刻飛行中飛機的位置,以此來詳細闡述姿態的計算。
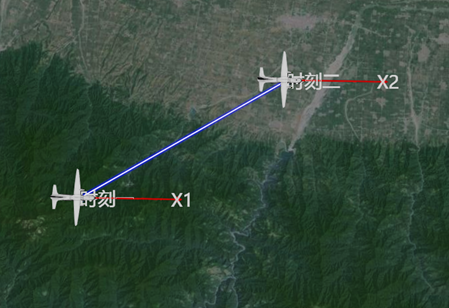
圖4 飛行中飛機的位置
上圖兩個時刻飛機的姿態都是初始狀態,即“東北天”姿態下,headingPitchRoll為(0,0,0),其中時刻一對應位置為“A點”,時刻二對應位置為“B點”。那么,如何計算飛機模型由“A點”朝向“B點”飛行姿態?
從圖中可以看出,只要在“A點”給飛機模型一個旋轉矩陣M,使飛機在模型坐標系下X軸與AB連線(藍色發光線)重合,即可實現飛機由A點向B點的飛行效果,因此我們可以先計算出旋轉矩陣M,再根據M計算飛機的飛行姿態。
Cesium中為我們提供了一個繞軸旋轉的接口,如下圖5,接口的返回值是一個四元數,我們將四元數轉換成矩陣即可,接口中的參數含義如下:
a) axis是旋轉軸;
b) angle是旋轉角度的弧度值;
c) result為返回的四元數,該值是繞旋轉軸axis旋轉angle角度后的四元數的值。
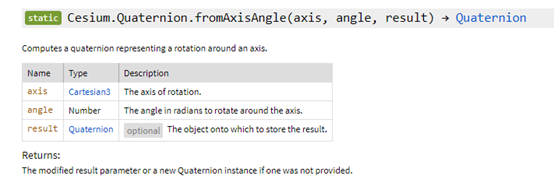
圖5
根據圖5接口入參的要求,我們需要正確的計算出旋轉軸(axis)和旋轉角度(angle)。由于先旋轉后平移,和先平移后旋轉的效果是完全不一樣的,且飛機從模型坐標到地球表面位置轉換中經過了旋轉和平移(圖4接口得到的矩陣變換),因此我們在計算圖5接口中的旋轉軸和旋轉角度時,需要考慮模型已經存在的旋轉和平移的影響。下面使用關鍵代碼詳細說明。
1) 計算模型坐標系下的航向向量
1. curAxis = Cesium.Cartesian3.subtract(pos2, pos1, curAxis);
計算時為了減少平移量的影響,我們使用相對坐標計算。首先設時刻一位置為pos1(x1,y1,z1,),時刻二位置為pos2(x2,y2,z2),那么,得到同一局部坐標系航向向量curAxis=(x2-x1,y2-y1,z2-z1)。
2. mat41 = = Cesium.Transforms.eastNorthUpToFixedFrame(pos1);
3. roatMat3 = Cesium.Matrix4.getRotation(mat41, roatMat3) ;
4. inveRoatMat3 = Cesium.Matrix3.inverse(roatMat3, inveRoatMat3)
5. curAxis = Cesium.Matrix3.multiplyByVector(inveRoatMat3,curAxis,curAxis);
計算模型坐標下航向向量。如上面代碼所示,因為從模型坐標到世界坐標經過了旋轉,我們要還原回去,所以我們需要獲取Cesium.Matrix4.getRotation(Cesium.Transforms.eastNorthUpToFixedFrame(pos1))的逆矩陣,乘以curAxis向量,得到在局部坐標系下的航向向量curAxis。
2) 計算旋轉軸和旋轉角度
1. //求旋轉軸
2. var axis = Cesium.Cartesian3.cross( vec1,vec2, new Cesium.Cartesian3(0,0,0));
3. orientMat = vec1ToVec2Mat(Cesium.Cartesian3.UNIT_X, Cesium.Cartesian3.normalize(curAxis,curAxis));//求夾角
4. var angle = Cesium.Math.acosClamped(Cesium.Cartesian3.dot(vec1, vec2)/
5. (Cesium.Cartesian3.magnitude(vec1)*Cesium.Cartesian3.magnitude(vec2) ) ) ;
旋轉軸我們可以通過X1向量和運動方向向量叉乘得到。vec1參數為X軸的單位向量,vec2參數為前面計算出來的模型坐標系下的航向向量curAxis。兩向量夾角根據公式cosθ=(向量a·向量b)/|向量a|×|向量b|計算出來。向量點乘(向量a·向量b)的值可以用Cesium.Cartesian3.dot(vec1, vec2)計算,向量模值可以用Cesium.Cartesian3.magnitude(vec1)計算。最后用Cesium.Math.acosClamped()計算反三角函數值,既夾角的弧度值。
3) 計算姿態角
6. //求四元數
7. var quaternion = Cesium.Quaternion.fromAxisAngle(axis,angle, new Cesium.Quaternion(0, 0, 0, 0));
8. //旋轉矩陣
9. var tHpr = Cesium.HeadingPitchRoll.fromQuaternion(quaternion, tHpr);
10. hpr = [Cesium.Math.toDegrees(tHpr.heading), Cesium.Math.toDegrees(tHpr.pitch), Cesium.Math.toDegrees(tHpr.roll)];
使用Cesium.Quaternion.fromAxisAngle()接口得到一個四元數,再使用Cesium.HeadingPitchRoll.fromQuaternion()接口計算出每個方向的姿態角。
完整的核心代碼如下:
11. //vec1 Cartesian3 vec2 Cartesian3
12. function vec1ToVec2Mat(vec1,vec2){
13. //求旋轉軸
14. var axis = Cesium.Cartesian3.cross( vec1,vec2, new Cesium.Cartesian3(0,0,0));
15. //求夾角
16. var angle = Cesium.Math.acosClamped(Cesium.Cartesian3.dot(vec1, vec2)/
17. (Cesium.Cartesian3.magnitude(vec1) *Cesium.Cartesian3.magnitude(vec2) ) ) ;
18. //求四元數
19. var quaternion = Cesium.Quaternion.fromAxisAngle(axis, angle, new Cesium.Quaternion(0, 0, 0, 0));
20. //旋轉矩陣
21. var rotMat3 = Cesium.Matrix3.fromQuaternion(quaternion, new Cesium.Matrix3());
22.
23. return rotMat3;
24. }
25.
26. mat41 = = Cesium.Transforms.eastNorthUpToFixedFrame(pos1);
27. var resQua = Cesium.Quaternion.clone(Cesium.Quaternion.IDENTITY);
28. var quaMatrix = Cesium.Matrix3.clone(Cesium.Matrix3.IDENTITY);
29. var roatMat3 = Cesium.Matrix3.clone(Cesium.Matrix3.IDENTITY);
30. var inveRoatMat3 = Cesium.Matrix3.clone(Cesium.Matrix3.IDENTITY);
31. var curAxis = new Cesium.Cartesian3(0,0,0);
32. roatMat3 = Cesium.Matrix4.getRotation(mat41, roatMat3) ;
33. var orientMat;
34. var hpr;
35. function computerOrient(){
36. curAxis = Cesium.Cartesian3.subtract(pos2, pos1, curAxis);
37. inveRoatMat3 = Cesium.Matrix3.inverse(roatMat3, inveRoatMat3)
38. curAxis = Cesium.Matrix3.multiplyByVector(inveRoatMat3,curAxis,curAxis);
39. orientMat = vec1ToVec2Mat(Cesium.Cartesian3.UNIT_X,
40. Cesium.Cartesian3.normalize(curAxis,curAxis));
41. resQua = Cesium.Quaternion.fromRotationMatrix(orientMat, resQua);
42. var tHpr = Cesium.HeadingPitchRoll.fromQuaternion(resQua, tHpr);
43. hpr = [Cesium.Math.toDegrees(tHpr.heading), Cesium.Math.toDegrees(tHpr.pitch),
44. Cesium.Math.toDegrees(tHpr.roll)];
45. }
46. computerOrient();
47. model2.modelMatrix = Cesium.Matrix4.multiplyByMatrix3(model2.modelMatrix,orientMat,model2.modelMatrix);
總結:通過上述對球心坐標系、模型坐標的介紹以及計算姿態角思路的梳理,已經可以讓動目標以正確的姿態運動了。
筆者水平有限,闡述不清之處還望讀者朋友見諒。有問題可以留言,我們的工作人員將會第一時間與您聯系,解決您的問題!















